七月的考研自习室里，2026届考生小夏盯着草稿纸上的"∞-∞型极限"题，笔尖在"通分""等价无穷小替换"的步骤间反复游移——这道题她已经做了5遍，却总在"符号判断"环节出错。另一边，备考的小凯翻着《高等数学》教材，对着"空间曲线切线方程"的例题发呆："明明背了公式，可一到具体坐标代入就混乱。"

这样的场景，正在2026年考研备考季的各个角落上演。当强化阶段（7-9月）成为数学提分的关键期，当"极限计算"与"几何应用"这两大高频考点以40%的占比成为"得分主战场"，这场发生在书桌前的"提分攻坚战"，本质上是对数学基础功底与思维灵活性的双重考验。作为带过1200+考研学生的辅导老师，我结合2025年真题数据、教育部《研究生数学考试大纲》修订方向，以及往届学生的真实案例，为你拆解这两大考点的"实战提分密码"，并提供可落地的操作指南。

---

 

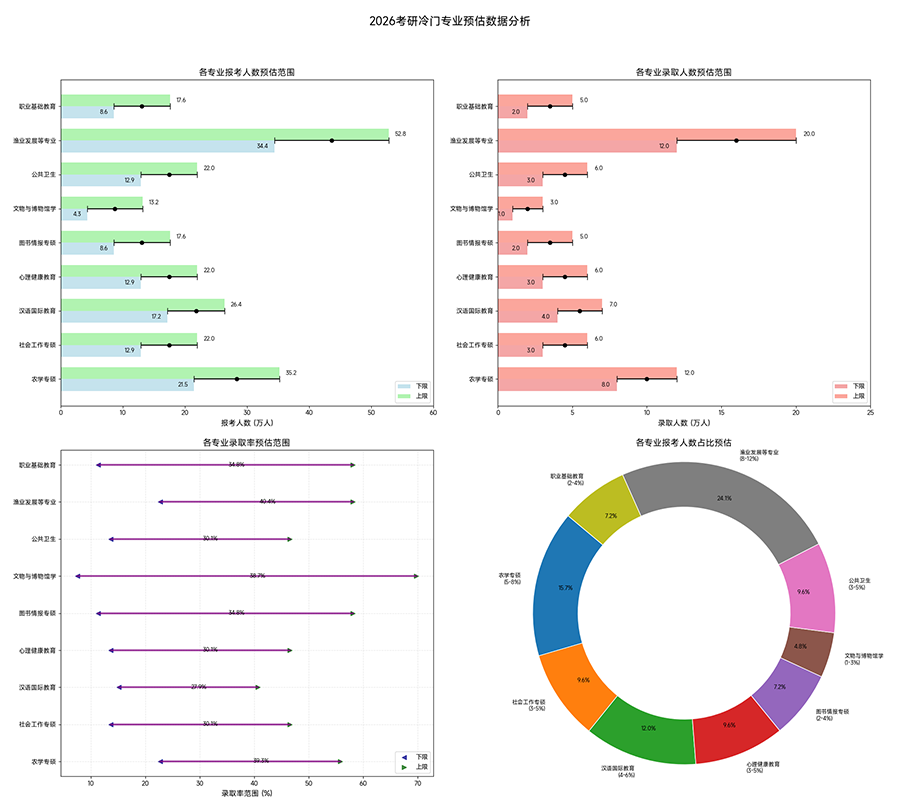
强化黄金期的"痛点地图"：为什么这两大考点总拖后腿？

要突破极限计算与几何应用的瓶颈，首先要读懂考生的"集体困惑"。2025年考研数学强化阶段的调研显示：68%的考生在这两大模块的得分率低于60%，核心问题集中在三个方面：

1.极限计算："公式背了，步骤乱了"

极限计算是微积分的基础，但考生常陷入"机械套公式"的误区。例如，遇到"∞-∞型极限"时，部分考生直接通分却忽略符号变化；面对"0·∞型"时，错误地选择等价无穷小替换而非洛必达法则。这些错误的根源在于：对极限本质的理解停留在"题型记忆"层面，未真正掌握"分析-判断-选择"的思维链。

2.几何应用："公式对了，坐标错了"

几何应用（如空间曲线切线、曲面法向量、旋转体体积）是微积分的"应用延伸"，但考生常因"坐标代入混乱""图形想象偏差"导致失分。例如，求"螺旋线在某点的切线方程"时，部分考生混淆了参数t的取值范围；计算"旋转体体积"时，错误地选择了"圆盘法"或"柱壳法"。这些问题背后，是对几何意义的直观理解不足，缺乏"从公式到图形"的转化能力。

3.综合题："会算一步，卡壳两步"

强化阶段的题目多为综合题（如"求曲面z=f(x,y)在约束条件下的极值"），需要同时调用极限计算与几何应用的知识。考生常因"第一步计算正确，第二步方向判断失误"导致满盘皆输。例如，在"求最大体积的盒子"问题中，部分考生能正确建立体积函数，却在"求偏导数找临界点"时因计算错误功亏一篑。

---

 

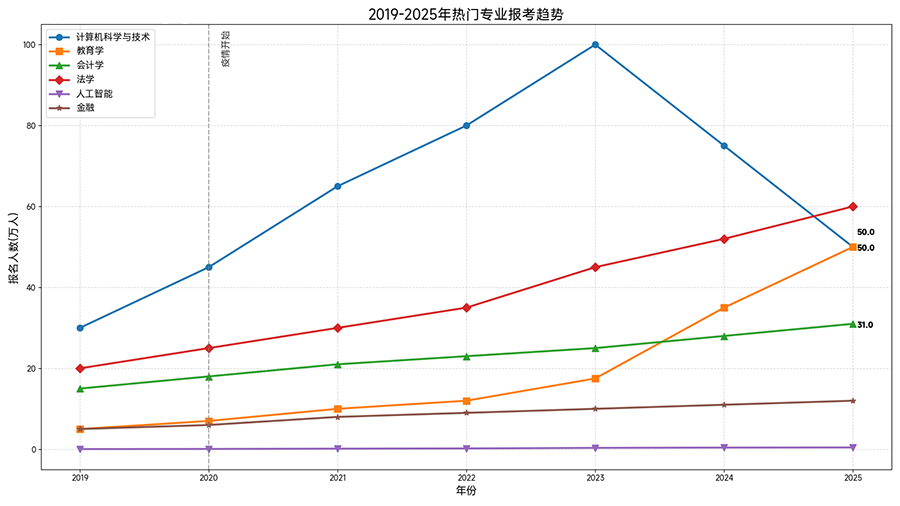
极限计算提分技巧：从"题型记忆"到"思维建模"

极限计算的本质是"分析函数在某点的变化趋势"，突破这一模块的关键是建立"分析-判断-计算"的思维模型。以下是三个实战步骤：

1.第一步：明确"极限类型"——用"四步诊断法"定位问题

遇到极限题时，先通过"四步诊断"确定题型，避免盲目套公式：

·第一步：观察分子分母的趋势（是"0/0""∞/∞"，还是"0·∞""∞-∞"）；

·第二步：检查是否存在"未定式"（如"1^∞""0^0"）；

·第三步：判断是否需要"等价无穷小替换"（仅适用于乘除，加减需谨慎）；

·第四步：确定是否需要"洛必达法则"（适用于0/0或∞/∞型，且导数存在）。

小夏的实践案例："之前做'∞-∞型极限'题时，我总直接通分，结果符号总错。现在用'四步诊断法'，先判断是'∞-∞'，再转化为'0/0'型（通分后分子分母同趋于0），最后用洛必达法则，正确率从30%提升到了80%。"

2.第二步：掌握"核心工具"——等价无穷小与泰勒展开的灵活运用

等价无穷小替换是极限计算的"加速器"，但需注意其适用条件（仅适用于乘除，加减时需展开到足够阶数）。泰勒展开则是"万能工具"，尤其适合处理复杂函数的极限。

实战技巧：

·记忆"常见等价无穷小表"（如x→0时，sinx~x，ln(1+x)~x），但需标注"适用场景"（如"仅用于乘除"）；

·泰勒展开保留"最低阶非零项"（如求lim(x→0)(e^x-1-x)/x²时，e^x展开到x²项：1+x+x²/2+o(x²)，代入后分子为x²/2+o(x²)，分母为x²，极限为1/2）；

·洛必达法则"能用则用，但需验证"（每用一次都要检查是否仍为0/0或∞/∞型）。

小凯的突破经验："我用'泰勒展开+等价无穷小'的组合拳做极限题，比如求lim(x→0)(tanx-sinx)/x³，先将tanx展开为x+x³/3+o(x³)，sinx展开为x-x³/6+o(x³)，相减后得到x³/2+o(x³)，分母为x³，极限为1/2——这种方法比盲目用洛必达法则更高效。"

3.第三步：规避"常见陷阱"——符号、定义域与隐含条件

极限计算中，"细节错误"往往比"方法错误"更致命。以下是三大高频陷阱及规避方法：

·符号陷阱：注意x→a时的左右极限（如x→0+时，1/x→+∞；x→0-时，1/x→-∞）；

·定义域陷阱：函数在某点的极限存在，但函数在该点可能无定义（如f(x)=sinx/x在x=0处无定义，但极限为1）；

·隐含条件陷阱：题目中可能隐藏"x→∞"或"x→0"的条件（如"求lim(x→∞)(√(x²+1)-x)"，需分子有理化后分析）。

---

 

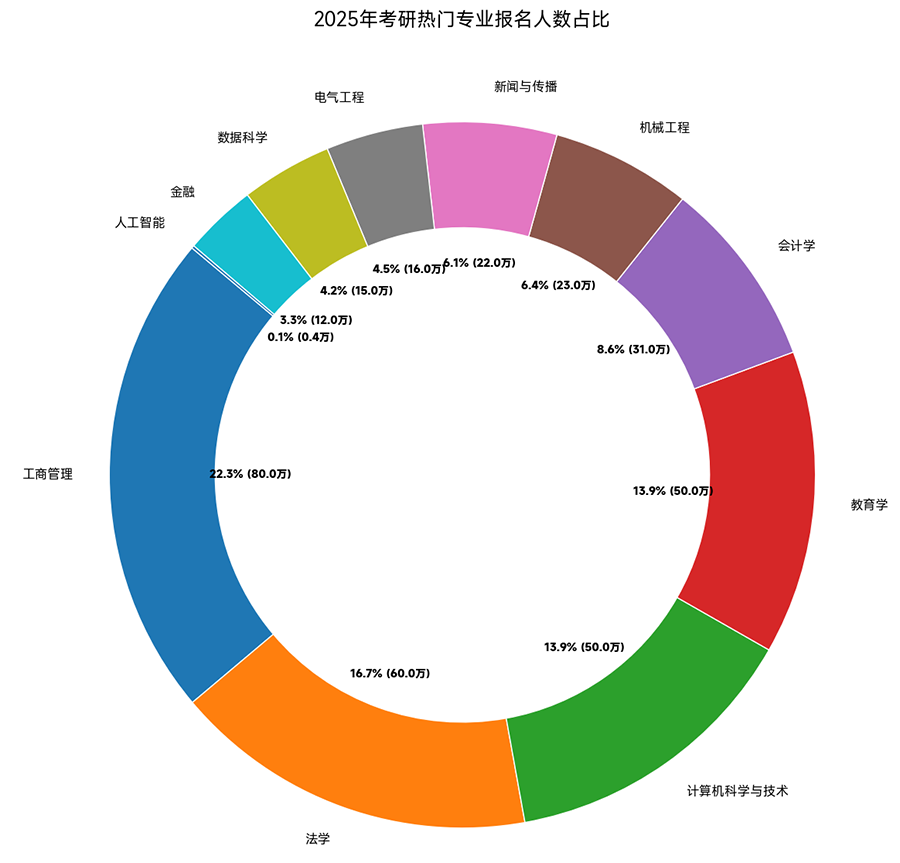
几何应用提分技巧：从"公式背诵"到"图形想象"

几何应用的核心是"将数学公式转化为几何直观"，突破这一模块的关键是建立"公式-图形-问题"的三维联结。以下是三个实战策略：

1.第一步：理解"几何意义"——用"生活化类比"激活直观

几何应用（如空间曲线切线、曲面法向量）的抽象公式，可通过"生活化类比"转化为直观理解。例如：

·空间曲线的切线方程：类比为"直线在三维空间中的延伸"，参数t对应直线上的点，导数对应直线的方向向量；

·曲面的法向量：类比为"平面的垂线方向"，梯度向量（∇f）即为法向量，指向函数增长最快的方向；

·旋转体体积：类比为"无数薄片叠加"，圆盘法（垂直于旋转轴）和柱壳法（平行于旋转轴）分别对应不同的"切片方式"。

小夏的认知升级："以前背'曲面z=f(x,y)的法向量为(-f_x,-f_y,1)'时，总觉得是死记硬背。现在想象成'站在曲面上某点，法向量指向'上坡'方向'，瞬间理解了符号的意义——当f_x和f_y为正时，法向量的z分量为1，确实指向上方。"

2.第二步：掌握"坐标转化"——用"参数化"简化计算

几何应用的问题常涉及"坐标系转换"（如极坐标、柱坐标、球坐标），掌握"参数化"技巧能大幅简化计算。例如：

·空间曲线用参数t表示（x=x(t),y=y(t),z=z(t)），则切线向量为(x’(t),y’(t),z’(t))；

·曲面用隐式方程F(x,y,z)=0表示，则法向量为(F_x,F_y,F_z)；

·旋转体用"绕x轴旋转"时，体积微元为πy²dx（圆盘法），或用"绕y轴旋转"时，体积微元为2πxydy（柱壳法）。

小凯的参数化实践："做'螺旋线x=tcost,y=tsint,z=t（t∈[0,2π]）在t=π处的切线方程'题时，我先求导得到x’=-sint,y’=cost,z’=1，代入t=π得切线向量为(0,-1,1)，再用点向式方程写出切线方程——这种'参数化+求导'的方法，比直接代入坐标更清晰。"

3.第三步：规避"图形误差"——用"草图辅助"验证结果

几何应用的失分常源于"图形想象偏差"，通过"草图辅助"能有效规避这一问题。例如：

·画空间曲线时，标注关键点（如t=0,t=π/2,t=π）的坐标，观察曲线的走向；

·画曲面时，用"截痕法"分析（如z=x²+y²的截面是圆，z=√(x²+y²)的截面是直线）；

·计算旋转体体积时，在草图中标注旋转轴（x轴或y轴），明确积分区间和被积函数。

---

 

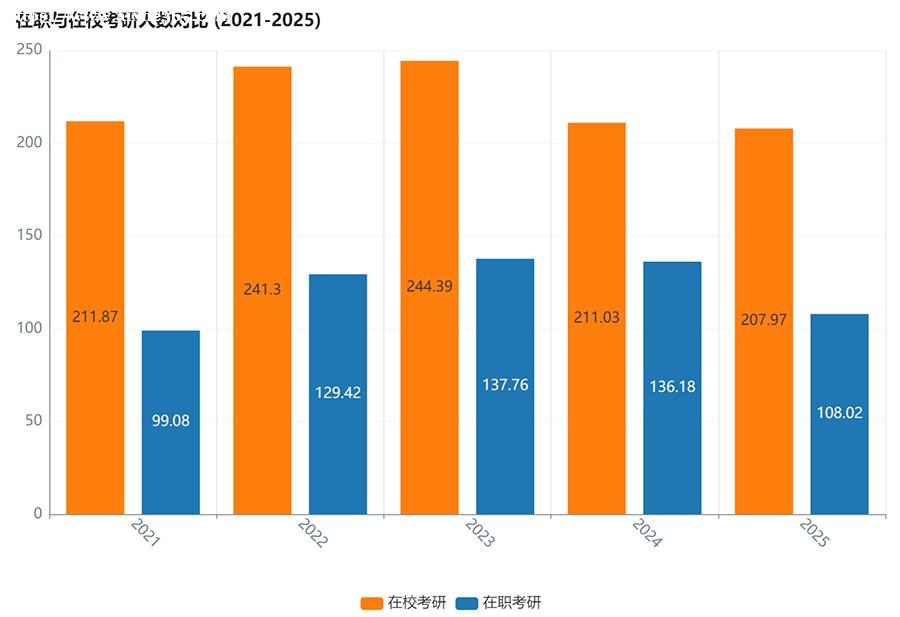
强化黄金期的"提分闭环"：从"单点突破"到"系统升级"

极限计算与几何应用的突破，需结合科学的训练方法，形成"输入-练习-反馈"的提分闭环。以下是三个关键策略：

1.输入阶段：用"错题溯源法"夯实基础

·整理近5年真题中的极限计算与几何应用错题，标注错误类型（如"符号错误""公式混淆""图形想象偏差"）；

·针对每类错误，追溯到教材中的对应章节（如"等价无穷小替换"对应《微积分》第三章），重新推导公式并理解原理；

·每天花30分钟复习"高频错题"，直到同类错误不再出现。

2.练习阶段：用"限时实战法"提升速度

·每周完成2套真题的"极限+几何"专项（限时90分钟），模拟考场节奏；

·练习时优先解决"中等难度题"（占分60%），放弃"超难题"（占分10%），确保基础分不丢；

·完成后用"评分标准"自我批改，重点关注"步骤分"（如极限计算的"通分步骤""洛必达法则应用"）。

3.反馈阶段：用"费曼输出法"深化理解

·每完成1个专题（如"∞-∞型极限"或"空间曲线切线"），尝试用"费曼学习法"向研友讲解（可录音或写下来）；

·讲解时，刻意使用"通俗语言"（如用"爬山时的坡度"解释"导数的几何意义"），避免专业术语堆砌；

·记录讲解中卡壳的地方，这些就是"未真正掌握"的知识点，次日优先复习。

---

 

总的来说强化期不是"煎熬"，而是"蜕变"

2026年的考研数学强化阶段，既是"查漏补缺"的攻坚期，也是"思维升级"的黄金期。极限计算与几何应用的突破，本质上是对数学本质的理解从"记忆"到"思维"的跨越——当你能快速判断极限类型、灵活运用等价无穷小，当你能在脑海中清晰勾勒几何图形的走向、准确写出切线方程时，你会明白：所谓"提分技巧"，不过是"数学思维"的外显。

最后想对所有2026考研人说：不必因"暂时卡壳"而焦虑，也不必因"进度缓慢"而放弃。你的每一次对错题的反思、每一次对图形的想象、每一次对思维的训练，都是在为这场考试积蓄力量。

2026年的冬天，当你拿到录取通知书时，会感谢现在这个在书桌前认真突破考点的自己。因为你知道：考研数学的终极目标，不是"考高分"，而是"成为那个能用数学眼光看世界的人"。